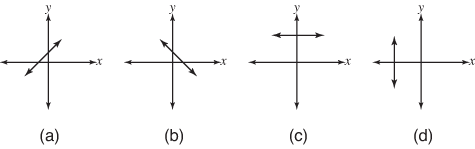
The slope of a line is a measurement of the steepness and direction of a nonvertical line. When a line slants from lower left to upper right, the slope is a positive number. Item (a) in Figure 1 shows a line with a positive slope. When a line slants from upper left to lower right, the slope is a negative number (b). The x‐axis or any line parallel to the x‐axis has a slope of zero; that is, a horizontal line has a slope of zero (c). The y‐axis or any line parallel to the y‐axis has no defined slope; that is, a vertical line has an undefined slope (d).
Figure 1. Slopes of lines.
If m represents the slope of a line and A and B are points lying on that line with coordinates ( x 1 ,y 1) and ( x 2 ,y 2), respectively, then the slope of the line passing through A and B is given by the following formula.
Since A and B cannot be points on a vertical line, x 1 and x 2 cannot be equal to one another. If x 1 = x 2, then the line is vertical, and the slope is undefined.
Example 1
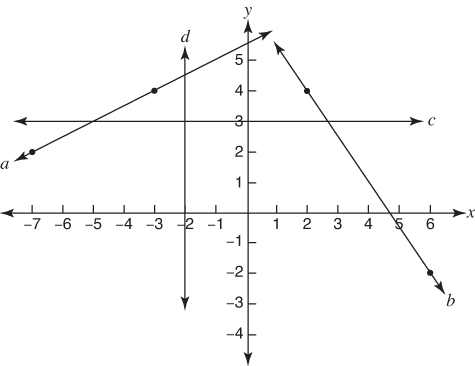
Use Figure 2 to find the slopes of the lines a, b, c, and d.
Line a passes through the points (–7,2) and (–3,4).
Line b passes through the points (2,4) and (6,–2).
Line c is parallel to the x‐axis. Therefore,
m = 0
Line d is parallel to the y‐axis. Therefore, line d has an undefined slope.
Figure 2. Find the slopes.
Example 2
A line passes through (–5,8) with a slope of 
. If another point on this line has coordinates ( x,12), find x.
