all that the absolute value of a number represents the distance that number is from zero on the number line. The equation | x| = 3 is translated as “ x is 3 units from zero on the number line.” Notice, on the number line shown in Figure 1, that two different numbers are 3 units away from zero, namely, 3 and –3.
Figure 1. Absolute value.
Absolute value.
The solution set of the equation | x| = 3 is {3, –3}, because |3| = 3 and |–3| = 3.
Example 1
Solve for x: |4 x – 2| = 8.
This translates to “4 x – 2 is 8 units from zero on the number line” (see Figure 2).
Check the solution.
These are true statements. The solution set is 
.
Figure 2. There are + and – solutions.
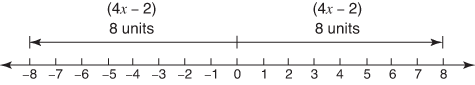
Example 2
Solve for x:
To solve this type of absolute value equation, first isolate the expression involving the absolute value symbol.
Now, translate the absolute value equation: “ 
is 11 units from zero on the number line.”
The check is left to you. The solution set is 
.
Example 3
Solve for x: | x | = –2.
This problem has no solutions, because the translation is nonsensical. Distance is not measured in negative values.
Example 4
Solve for x: |2 x – 3| = |3 x + 7|.
This type of sentence will be true if either
-
The expressions inside the absolute value symbols are exactly the same (that is, they are equal); or
-
The expressions inside the absolute value symbols are opposites of each other.
The check is left to you. The solution set is 
.
Example 5
Solve for x: | x – 2| = |7 – x|.
The sentence –2 = –7 is never true, so it gives no solution. So the only possible solution is 
.
Check the solution.
Therefore, the solution set is 
.