In Figure 1, A has coordinates (2,2), B has coordinates (5,2), and C has coordinates (5,6).
Figure 1. A right triangle.
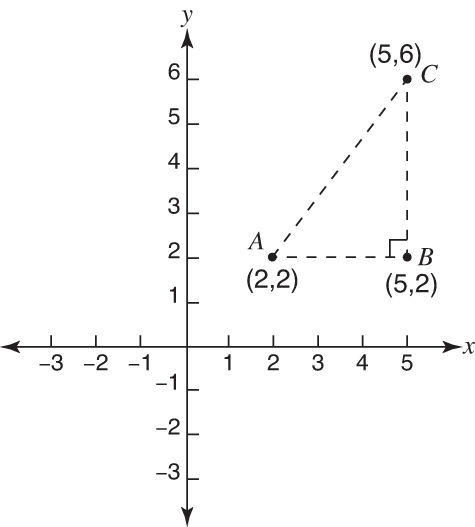
To find the length of AB or BC, only simple subtraction is necessary.

To find the length of AC, however, simple subtraction is not sufficient. Triangle ABC is a right triangle with AC being the hypotenuse. Therefore, by the Pythagorean theorem,

From the Pythagorean theorem, we derive the distance formula, which is nothing more than a different format for the former. If A is represented by the ordered pair ( x 1 ,y 1) and C is represented by the ordered pair ( x 2 ,y 2), then 
Then 

d in the preceding formula stands for distance.
Example 1
Use the distance formula to find the distance between the points with coordinates (–3,4) and (5,2).
Let (–3,4) = ( x 1 ,y 1) and (5,2) = ( x 2 ,y 2). Then 