Another way to look at enzymes is with an initial velocity plot. The rate of reaction is determined early in the progress curve—very little product is present, but the enzyme has gone through a limited number of catalytic cycles. In other words, the enzyme is going through the sequence of product binding, chemical catalysis, and product release continually. This condition is called the steady state. For example, the three curves in Figure represent progress curves for an enzyme under three different reaction conditions. In all three curves, the amount of enzyme is the same; however, the concentration of substrate is least in curve (a), greater in curve (b), and greatest in curve (c). The progress curves show that more product forms as more substrate is added. The slopes of the progress curves at early time, that is, the rate of product formation with time also increase with increasing substrate concentration. These slopes, called the initial rates or initial velocities, of the reaction also increase as more substrate is present so that:
The more substrate is present, the greater the initial velocity, because enzymes act to bind to their substrates. Just as any other chemical reaction can be favored by increasing the concentration of a reactant, the formation of an enzyme‐substrate complex can be favored by a higher concentration of substrate.

Figure 2
A plot of the initial velocities versus substrate concentration is a hyperbola (Figure ). Why does the curve in Figure flatten out? Because if the substrate concentration gets high enough, the enzyme spends all its time carrying out catalysis and no time waiting to bind substrate. In other words, the amount of substrate is high enough so that the enzyme is saturated, and the reaction rate has reached maximal velocity, or V max. Note that the condition of maximal velocity in Figure is not the same as the state of thermodynamic equilibuium in Figures 1 and 2.

Figure 3
Although it is a velocity curve and not a binding curve, Figure is a hyperbola. Just as myoglobin is saturated with oxygen at high enough pO 2, so an enzyme is saturated with substrate at high enough substrate concentration, designated [S]. The equation describing the plot in Figure is similar in form to the equation used for O 2 binding to myoglobin:
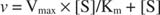
K m is the Michaelis constant for the enzyme binding substrate. The Michaelis constant is analogous to, but not identical to, the binding constant for the substrate to the enzyme. V max is the maximal velocity available from the amount of enzyme in the reaction mixture. If you add more enzyme to a given amount of substrate, the velocity of the reaction (measured in moles of substrate converted per time) increases, because the increased amount of enzyme uses more substrate. This is accounted for by the realization that V max depends on the total amount of enzyme in the reaction mixture:
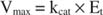
where E t is the total concentration of the enzyme and k cat is the rate constant for the slowest step in the reaction.
Other concepts follow from the Michaelis‐Menten equation. When the velocity of an enzymatic reaction is one‐half the maximal velocity: 
then:
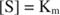
because:
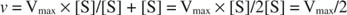
In other words, the K m is numerically equal to the amount of substrate required so that the velocity of the reaction is half of the maximal velocity.
Alternatively, when the concentration of substrate in the reaction is very high (V max conditions), then [S] >> K m, and the K m term in the denominator can be ignored in the equation, giving:
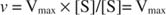
On the other hand, when [S] << K m, the term [S] in the denominator of the Michaelis‐Menten equation can be ignored, and the equation reduces to:
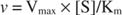
In the last case, the enzyme is said to be under first order conditions, because the velocity depends directly on the concentration of substrate.
In the terms of the Michaelis‐Menten equation, inhibitors can raise K m, lower V max, or both. Inhibitors form the basis of many drugs used in medicine. For example, therapy for high blood pressure often includes an inhibitor of the angiotensin converting enzyme, or ACE. This enzyme cleaves (hydrolyzes) angiotensin I to make angiotensin II. Angiotensin II raises blood pressure, so ACE inhibitors are used to treat high blood pressure. Another case is acetylsalicylic acid, or aspirin. Aspirin successfully treats inflammation because it covalently modifies, and therefore inactivates, a protein needed to make the signaling molecule that causes inflammation.
The principles behind enzyme inhibition are illustrated in the following examples.
Alkaline phosphatase catalyzes a simple hydrolysis reaction:
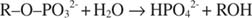
Phosphate ion, a product of the reaction, also inhibits it by binding to the same phosphate site used for binding substrate. When phosphate is bound, the enzyme cannot bind substrate, so it is inhibited by the phosphate. How to overcome the inhibitor? Add more substrate: R –O –PO 3 2‐. Because the substrate and the inhibitor bind to the same site on the enzyme, the more substrate that binds, the less inhibitor binds. When is the most substrate bound to the enzyme? Under V max conditions. Phosphate ion reduces the velocity of the alkaline phosphate reaction without reducing V max. If velocity decreases, but V max doesn't, the only other thing that can change is K m. Remember that K m is the concentration where v= V max/2. Because more substrate is required to achieve V max, K m must necessarily increase. This type of inhibition, where K m increases but V max is unchanged, is called competitive because the inhibitor and substrate compete for the same site on the enzyme (the active site).
Other cases of inhibition involve the binding of the inhibitor to a site other than the site where substrate binds. For example, the inhibitor can bind to the enzyme on the outside of the protein and thereby alter the tertiary structure of the enzyme so that its substrate binding site is unable to function. Because some of the enzyme is made nonfunctional, adding more substrate can't reverse the inhibition. V max, the kinetic parameter that includes the E t term, is reduced. The binding of the inhibitor can also affect K m if the enzyme‐inhibitor complex is partially active. Inhibitors that alter both V max and K m are called noncompetitive; the rare inhibitors that alter V max only are termed uncompetitive.
You can visualize the effects of inhibitors using reciprocal plots. If the Michaelis‐Menten equation is inverted:
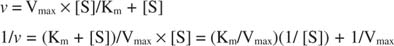
This equation is linear and has the same form as:
so that a plot of 1/ v versus 1/[S] (a Lineweaver‐Burk plot, shown in Figure ) has a slope equal to K m/V max and a y‐intercept equal to 1/V max. The x‐intercept of a Lineweaver‐Burk plot is equal to ‐1/K m.

Figure 4
Competitive inhibitors decrease the velocity of an enzymatic reaction by increasing the amount of substrate required to saturate the enzyme; therefore, they increase the apparent K m but do not affect V max. A Lineweaver‐Burk plot of a competitively inhibited enzyme reaction has an increased slope, but its intercept is unchanged.
Noncompetitive inhibitors both increase the apparent K m and reduce the apparent V max of an enzyme‐catalyzed reaction. Therefore, they affect both the slope and the y‐intercept of a Lineweaver‐Burk plot, as Figures and show. Uncompetitive inhibitors, because they reduce V max only, increase the reciprocal of V max. The lines of the reciprocal plot are parallel in this case.

Figure 5

Figure 6
Covalent inhibition involves the chemical modification of the enzyme so that it is no longer active. For example, the compound diisopropylfluorophosphate reacts with many enzymes by adding a phosphate group to an essential serine hydroxyl group in the enzymes' active sites. When phosphorylated, the enzyme is totally inactive. Many useful pharmaceutical compounds work by covalent modification. Aspirin is a covalent modifier of enzymes involved in the inflammatory response. Penicillin covalently modifies enzymes required for bacterial cell‐wall synthesis, rendering them inactive. Because the cell wall is not able to protect the bacterial cell, the organism bursts easily and is killed.