Solving General Triangles

The process of solving triangles can be categorized into several distinct groups. The following is a listing of these categories along with a procedure to follow to solve for the missing parts of the triangle. The assumption is made that all three missing parts are to be found. If only some of the unknown values are to be determined, a modified approach may be in order.

SSS: If the three sides of a triangle are known, first use the Law of Cosines to find one of the angles. It is usually best to find the largest angle first, the one opposite the longest side. Then, set up a proportion using the Law of Sines to find the second angle. Finally, subtract these angle measures from 180° to find the third angle.
The reason that the Law of Cosines should be used to find the largest angle in the triangle is that if the cosine is positive, the angle is acute. If the cosine is negative, the angle is obtuse. If the cosine is zero, the angle is a right angle. Once the largest angle of the triangle is known, the other two angles must be acute.
If the largest angle is not found by using the Law of Cosines but by using the Law of Sines instead, the determination whether the angle is acute or obtuse must be done using the Pythagorean theorem or other means because the sine is positive for both acute (first quadrant) and obtuse (second quadrant) angles. This adds an extra step to the solution of the problem.
If the size of only one of the angles is needed, use the Law of Cosines. The Law of Cosines may be used to find all the missing angles, although a solution using the Law of Cosines is usually more complex than one using the Law of Sines.
SAS: If two sides and the included angle of a triangle are known, first use the Law of Cosines to solve for the third side. Next, use the Law of Sines to find the smaller of the two remaining angles. This is the angle opposite the shortest or shorter side, not the longest side. Finally, subtract these angle measures from 180° to find the third angle. Again, you can use the Law of Cosines to find the two missing angles, although a solution using the Law of Cosines is usually more complex than one using the Law of Sines.
ASA: If two angles and the included side of a triangle are known, first subtract these angle measures from 180° to find the third angle. Next, use the Law of Sines to set up proportions to find the lengths of the two missing sides. You can use the Law of Cosines to find the length of the third side, but why bother if you can use the Law of Sines instead?
AAS: If two angles and a nonincluded side of a triangle are known, first subtract these angle measures from 180° to find the third angle. Next, use the Law of Sines to set up proportions to find the lengths of the two missing sides. The given side is opposite one of the two given angles. If all that is needed is the length of the side opposite the second given angle, then use the Law of Sines to calculate its value.
SSA: This is known as the ambiguous case. If two sides and a nonincluded angle of a triangle are known, there are six possible configurations, two if the given angle is obtuse or right and four if the given angle is acute. These six possibilities are shown in Figures 1 2 and 3 . In Figures and , h is an altitude where h = a sin β and β is an acute angle.

Figure 1
Two cases for SSA.

Figure 2
Ambiguous cases for SSA.

Figure 3
Two cases for SSA.

In Figure 1(a), if b < h, then b cannot reach the other side of the triangle, and no solution is possible. This occurs when b < a sin β.

In Figure 1 (b), if b = h = a sin β, then exactly one right triangle is formed.

In Figure 2 (a), if h < b < a—that is, a sin β < b, < a—then two different solutions exist.

In Figure 2 (b), if b = a, then only one solution exists, and if b = a, then the solution is an isosceles triangle.

If β is an obtuse or right angle, the following two possibilities exist.

In Figure 3 (a), if b > a, then one solution is possible.

In Figure 3 (b), if b ≤ a, then no solutions are possible.

Example 1: (SSS) Find the difference between the largest and smallest angles of a triangle if the lengths of the sides are 10, 19, and 23, as shown in Figure 4 .

Figure 4
Drawing for Example 1.

First, use the Law of Cosines to find the size of the largest angle (β) which is opposite the longest side (23).

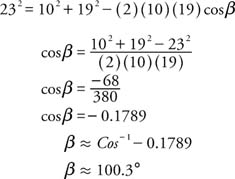
Next, use the Law of Sines to find the size of the smallest angle (α), which is opposite the shortest side (10).

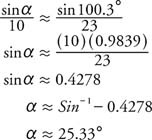
Thus, the difference between the largest and smallest angle is

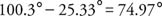
Example 2: (SAS) The legs of an isosceles triangle have a length of 28 and form a 17° angle (Figure 5). What is the length of the third side of the triangle?

Figure 5
Drawing for Example 2.

This is a direct application of the Law of Cosines.

Example 3: (ASA) Find the value of d in Figure 6 .

Figure 6
Drawing for Example 3.

First, calculate the sizes of angles α and β. Then find the value of a using the Law of Sines. Finally, use the definition of the sine to find the value of d.

Finally,

Example 4: (AAS) Find the value of x in Figure 7 .

Figure 7
Drawing for Example 4.

First, calculate the size of angle α. Then use the Law of Sines to calculate the value of x.

Example 5: (SSA) One side of a triangle, of length 20, forms a 42° angle with a second side of the triangle (8). The length of the third side of the triangle is 14. Find the length of the second side.

Figure 8
Drawing for Example 5.

The length of the altitude (h) is calculated first so that the number of solutions (0, 1, or 2) can be determined.

Because 13.38 < 14 < 20, there are two distinct solutions.

Solution 1: Use of the Law of Sines to calculate α.

Use the fact that there are 180° in a triangle to calculate β

Use the Law of Sines to find the value of b.

Solution 2: Use α to find α′, and α′ to find β′

Next, use the Law of Sines to find b′.

Trigonometry

Solving General Triangles